Dr. Cesar Maldonado.
Investigador División de Control y Sistemas Dinámicos del IPICYT
«[…]¿No es acaso tu irreversible tiempo el de aquel río
en cuyo espejo Heráclito vio el símbolo de su fugacidad?
Te espera el mármol que no leerás. En él ya están escritos
la fecha, la ciudad y el epitafio.»
Jorge Luis Borges
En su poema, Borges habla del tiempo irreversible y nos recuerda a Heráclito que al mirar el agua fluir, concluye que no puede bañarse dos veces en el mismo río. Nada permanece, sólo el cambio. Nos habla también de un fatal desenlace, nos hace ver que hay una flecha en el tiempo, una dirección a la que poco a poco nos encaminamos. Estamos tan acostumbrados a ese sentido temporal que cuando vemos algo en reversa nos parece curioso, fantástico o completamente irreal. De ahí la genialidad de Francis Scott Fitzgerald de imaginarse a una persona que va rejuveneciendo con el paso del tiempo en su cuento «El curioso caso de Benjamin Button», que después sería llevado al cine protagonizado por Brad Pitt.
Hablando de irreversibilidad y de cine, cómo no recordar a la película de Gaspar Noé llamada, justamente: «Irreversible». En ella nos cuenta la historia desde el final hacia el principio, que no deja de deslumbrarnos y atormentarnos por su crudeza, aún cuando desde el inicio de la película ya sabemos cómo termina la historia, o más bien, muy a pesar de ello. La gran mayoría de los fenómenos que ocurren en nuestro entorno son irreversibles, ahí radica el gran mérito tanto de Gaspar Noé como de Fitzgerald, porque en su discurso rompen con el sentido del paso de las cosas al que estamos acostumbrados. Para nosotros, el río fluye en una dirección y, a menos que una gran catástrofe climática ocurra, ésta no cambia. Las cosas que se caen se rompen en pedazos, una gota de tinta en agua se diluye, nuestro café se enfría y nosotros, muy a nuestro pesar; envejecemos.
De ahí la importancia de entender y describir los fenómenos irreversibles. Esos fenómenos en los cuales podemos distinguir claramente cuál es su inicio y cuál es su fin, o en los que sabemos ordenar temporalmente los sucesos. Es por eso por lo que las y los físicos se han puesto a la tarea de formalizar estos fenómenos y de establecer las leyes que los rigen, de clasificarlos y cuantificarlos. Desde el punto de vista matemático, hay también muchas preguntas fundamentales al respecto. Desde entender por qué la naturaleza misma tiene una dirección preferencial en el tiempo (¿de verdad la tiene?). O simplemente dar una definición rigurosa y precisa de la irreversibilidad desde las matemáticas. Con esta idea, las personas de ciencia han logrado construir todo un conjunto de teorías que dan fundamento teórico a los fenómenos de los sistemas que están fuera del equilibrio (y también por supuesto, a aquellos en equilibrio) y, aunque aún falta mucho por hacer; hay un buen camino recorrido.
Pero ¿de qué nos sirve tener definiciones precisas o fórmulas exactas de sistemas simplificados?, bueno, pues porque si tenemos a nuestra disposición modelos claros y bien entendidos, podemos internar aplicarlos a fenómenos reales que, en su gran mayoría, son mucho más complejos que los simples modelos matemáticos. Por ejemplo, los procesos biológicos que rigen nuestro cuerpo, los que gobiernan al clima o los procesos geológicos, las reacciones químicas, los movimientos en la bolsa de valores, en fin, la gran mayoría de los fenómenos de interés práctico resulta que son fenómenos irreversibles y también bastante complejos. Una de las formas más usadas por las matemáticas aplicadas es analizar los datos provenientes de algún experimento u observación de un fenómeno en forma de series de tiempo. Esto es, anotando las mediciones de la observable de interés a intervalos bien definidos de duración. Con esto se obtiene una gráfica de la variación en el tiempo de la cantidad observada. Una vez que tenemos modelos matemáticos sencillos, podemos tomar estos datos de los fenómenos de estudio y darles alguna interpretación a partir de nuestros modelos teóricos. En el mejor de los casos, lograremos entenderlos y predecir comportamientos futuros del fenómeno en cuestión. En pocas palabras, de esto se trata el análisis de series de tiempo.

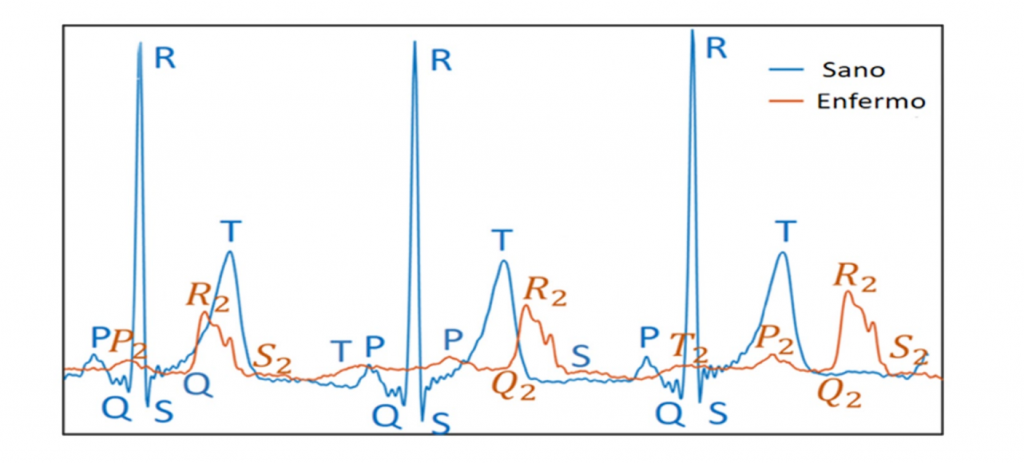
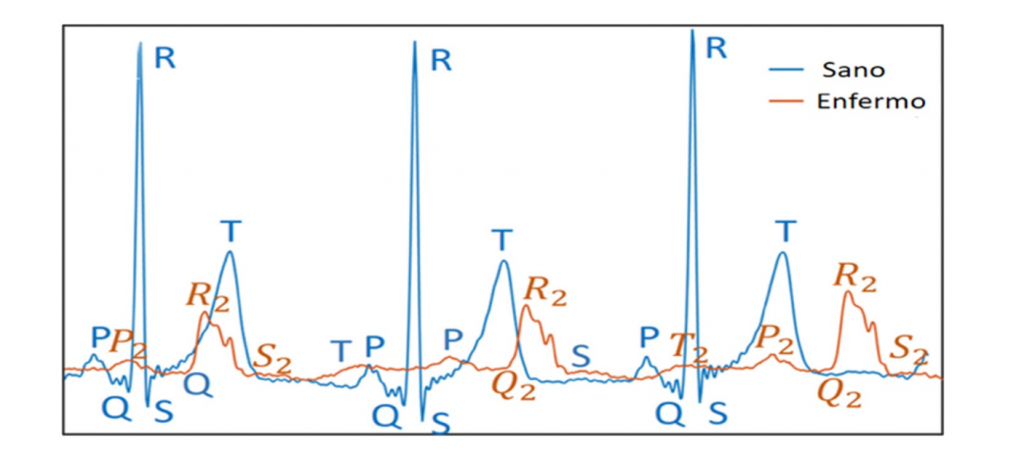
Ya que hablamos un poco de sistemas irreversibles y de series de tiempo, ahora podemos entrar en detalle al sistema que estudian algunos grupos de investigación en la División de Control y Sistemas Dinámicos del Instituto Potosino de Investigación Científica y Tecnológica (IPICYT). Esto es, el estudio de irreversibilidad en series de tiempo en electrocardiogramas. La gran mayoría de nosotros hemos visto esas señales que detectan la actividad eléctrica cardíaca y que conocemos como electrocardiogramas. El más común de ellos muestra ondas (llamadas ondas P, Q, R, S y T, principalmente) que, en una persona sana; son bastante regulares, tienen una duración y una amplitud bien conocida por los médicos y además tienen una periodicidad y fluctuaciones alrededor de esos valores normales muy bien estudiadas. Resulta que estas señales, son series de tiempo de un fenómeno irreversible. Hay una dirección clara y bien determinada en el orden de aparición de esas ondas y, al menos en una persona sana, no es lo mismo mirar estas gráficas en un sentido que mirarlas en el sentido inverso.
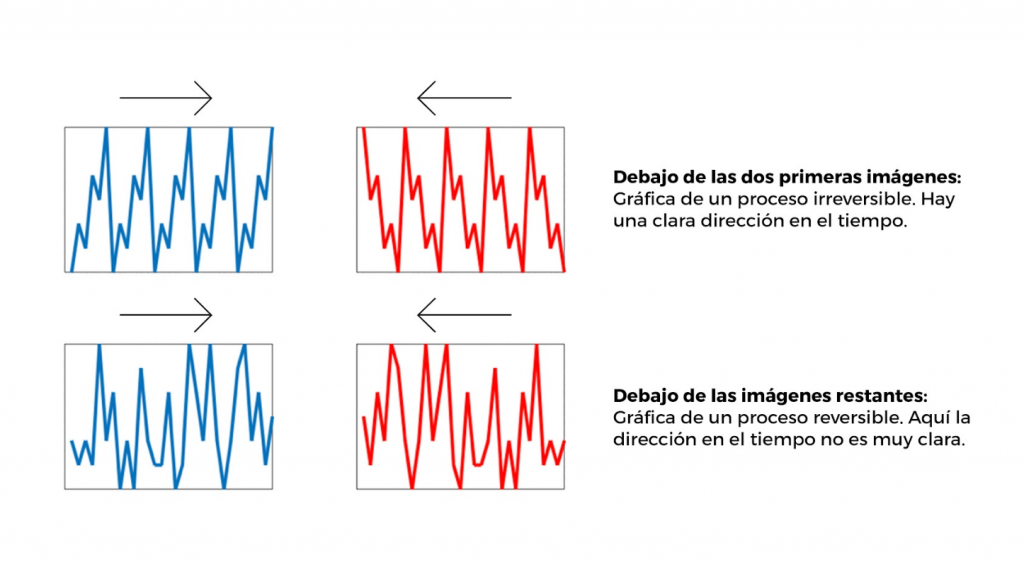
Ahora, ¿qué pasaría en el caso de una persona con problemas severos en el corazón? Podemos intuir que las señales de su actividad eléctrica cardíaca serán mucho más “ruidosas” por así decirlo, menos organizadas, menos regulares en su periodicidad y con fluctuaciones mayores en la amplitud de las ondas. Esto es, que la serie de tiempo luciría más desordenada. En un caso extremo, sería difícil identificar cuál es la dirección correcta de la lectura de los datos en una serie de tiempo de esta persona con problemas de salud. Es por esto por lo que, una de las hipótesis planteadas en el análisis de los electrocardiogramas es precisamente que una persona sana presenta un grado mayor de irreversibilidad en su actividad eléctrica que una persona con alguna condición médica de gravedad. Antes de continuar, detengámonos un poco en esta idea que puede parecer contradictoria. Como mencionamos al principio, cuando un fenómeno es irreversible, si lo vemos en sentido inverso en el tiempo, notamos algo extraño, podemos saber que el tiempo está corriendo hacia atrás. En el caso de una persona sana, sabemos qué orden llevan las ondas que componen su electrocardiograma, son muy regulares y no hay forma de confundir una onda con otra porque conservan sus propiedades típicas de amplitud y duración. Si pusiéramos su electrocardiograma en el sentido inverso, de inmediato nos percatamos de que lo estamos viendo al revés, es decir que su señal electrocardiográfica es irreversible. En cambio, si tenemos una señal eléctrica muy errática, no podremos distinguir su dirección en el tiempo, porque unas ondas se parecen a las otras, porque se pierde el estricto ritmo que tiene una persona sana, entre otros fenómenos adversos. Es como si nos dan un vaso con una gota de tinta, pero que ya se encuentra completamente diluida. Si nos esperamos un poco más, la tinta seguirá igual de diluida y si grabáramos todo ese lapso y lo vemos hacia atrás, no podremos distinguir cuál fue el inicio y cuál el final. Es decir, nos topamos con un fenómeno que se encuentra en estado de reversibilidad temporal.
Y aquí es donde entran en juego las matemáticas. Para analizar a profundidad estas series de tiempo, recurrimos a la teoría de las probabilidades, así como a los sistemas dinámicos para proponer estimadores de índices de irreversibilidad que nos permitan distinguir entre personas sanas y personas con alguna condición médica usando únicamente los datos. Claro que los ojos de los médicos están bien entrenados para hacer esta tarea, pero tenemos la esperanza de que con las herramientas que se pueden desarrollar desde las matemáticas, en un futuro no muy lejano podríamos contar con sistemas de detección de enfermedades cardiacas incluso en etapas tempranas. Por ahora, lo importante es seguir desarrollando la teoría desde la ciencia básica y la aplicada para que, en efecto; pronto podamos ver los resultados prácticos en beneficio de la calidad de vida humana. Y que, aunque como dijo Borges, de igual manera nos espera el mármol donde está escrito, la fecha, la ciudad y el epitafio; y aunque no podamos rejuvenecer como Benjamin Button, al menos que nuestro transcurrir por el tiempo irreversible sea más placentero.
¿Te gustaría conocer más información sobre el tema? Envía un correo electrónico al Dr. Cesar O. Maldonado: cesar.maldonado@ipicyt.edu.mx
¿Quieres conocer más del IPICYT? Contáctanos: comunicacion@ipicyt.edu.mx